简谐振动的运动学特征
王玉君 程春晓
章节名称 | 简谐振动的运动学 |
授课对象 | 本科工科各专业大一/大二学生 | 教学环境 | 智慧教室 |
教学目标 | 1. 知识目标 | 掌握描述简谐振动的特征量及各量之间的关系，简谐振动的运动学方程的基本特征； 能确定振动方程中的三个特征量：振幅、初位相和角频率； 能用解析法、图形法及旋转矢量法解物体简谐振动运动状态的方法。 |
2. 能力目标 | 提高学生发现问题、提出问题和分析解决问题的能力。 |
3. 素质目标 | 引导学生树立科学的世界观，激发学生的求知热情、探索精神、创新欲望，以及敢于向旧观念挑战的精神。 |
4. 育人目标 | 培养学生探索精神； 培养学生创新意识。 |
教学重点 | 简谐振动中的三个重要参量(振幅、周期、位相和初位相)、简谐振动的旋转矢量表示法 |
教学难点 | 由已知条件利用解析法或旋转矢量法求出简谐振动方程 |
教学方法 | 讨论式、启发式、讲练结合 |
思政要素 | 1. 在“导入新课”时，介绍港珠澳跨海大桥、雅安—西昌高速公路的防震设计。让学生了解中国的科技发展，建立文化自信。 2. 在“应用举例”中，介绍简谐振动在车辆悬挂系统、建筑物结构中的减震设计和无线电通信方面等的应用。重点介绍在地震频繁的地区或高楼大厦中，为了减少结构受到地震力的影响，常常会采用简谐振动减震设计。通过在建筑物结构中设置特定的减震装置，可以将地震引起的动能转化为其他形式的能量，减轻地震对建筑物的破坏程度，提高建筑的抗震性能。让学生了解到物理是源于生活也是解决生活问题的基本工具，进而增加学生的感性认识。 3. 在“拓展提升”中，介绍相位命名的来历，体会中华文化的博大精深。在讲授利用旋转矢量法求出简谐振动方程时，让学生体会通过“已知”探索“未知”的乐趣。感知解决问题多途径，处理问题要敢于另辟蹊径，培养学生的创新性思维。 |
参考资料 | 1、马文蔚.《物理学》第四版. 北京.高等教育出版社，2002.07. 2、程守洙.《普通物理学》第六版. 北京.高等教育出版社，2006.12. 3、中国大学慕课上国家精品课程-山东大学的《大学物理》. |
|
|
|
|
|
“简谐振动的运动学”教学过程设计
一、创设情境、导入新课 —— 港珠澳跨海大桥、雅安—西昌的雅西高速公路的防震设计
桥梁在风、水流、地震等作用下，会产生震动。当震动超过一定幅度，就会导致大桥受损甚至垮塌。通过合理的设计，选择合适的建筑材料，才能保证桥梁的安全。
港珠澳跨海大桥
港珠澳跨海大桥为防止台风、洋流冲击对桥梁造成的震动损害，特意修成具有一定的弯曲度。
雅安—西昌高速公路：“云端上的公路”。
雅西高速地处地震带，为防止地震波对公路路基桥墩造成破坏，特意把比较高的公路桥墩不用混凝土建造，而是采用钢结构建造：相比混凝土，钢材具有更大弹性形变能力，可以在地震来临时很好的保证桥梁安全。
作为举世闻名的基建狂魔，中国创造了一个又一个桥梁、公路建设中的“不可能”！
让学生了解中国科技的发展，建立文化自信。
【教学策略】导入新课时，引入港珠澳跨海大桥、雅安高速，让学生感受我国的科技进步，建立文化自信，鼓励学生走在科学技术发展的前沿，弘扬社会主义人文精神。
二、理论推导、探究新知 —— 简谐振动的运动学
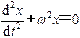1.简谐振动的运动学方程
微分方程
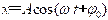
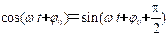简谐振动的运动学方程
由于
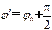令
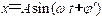则
2.描述简谐振动的三个重要参量
（1）振幅
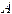最大位移的绝对值 ( 恒为正)。
（2）周期、频率、角频率
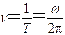
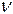
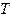周期 为振动一次所需时间；频率 为单位时间的振动次数， ；角频率为2 π秒内完成的完全振动的次数。
（3）相位和初相位
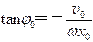
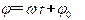相位为能确定系统任意时刻振动状态的物理量， ；
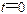初相为 时的相位 ， ；
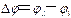相位差为两简谐振动相位之差， 。
3.旋转矢量表示法
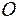
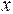
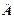以 点为原点旋转矢量 的端点在 轴上的投影点的运动为简谐运动。
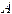振幅：旋转矢量的模 ；
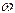角频率：旋转矢量逆时针转动的角速度 ；
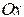
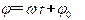相位：旋转矢量与 轴夹角 。
【教学策略】1.通过由浅入深的讨论得到简谐振动的运动学方程，并扩展讨论至每一个描述简谐运动的物理量，引导学生进行演绎思维的训练；2. 给出旋转矢量表示的方法，引导学生发现自然真理的公式抽象并能够欣赏自然的简单美，引导学生更深层的思考和探究，调动学生积极参与课堂中，完成知识的深入理解和内化。
三、应用举例——简谐振动的运动学方程及其应用
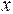
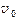
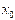
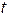
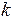例1一个理想的弹簧振子，弹簧的劲度系数 =0.72 N·m-1，振子的质量为0.02 kg， =0时，振子在 =0.05m处，初速度 =0.30 m·s-1，且沿 轴正向运动，求：
(1) 振子的运动方程；
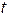(2) 振子在 = π/4 s时的速度和加速度。
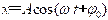解：(1) 因为振子作简谐运动，所以可设它的运动方程为
根据振动系统的固有条件，可求出角频率
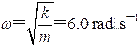
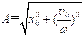
由振动系统初始条件及公式 可求出振幅
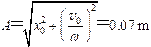
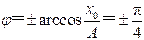
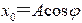则
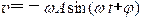
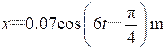
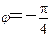
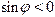
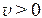
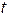由于初相只能是[0 ，2π）或[-π ，π）中唯一的值，再由 ，当 =0时， ，则只有 ，因而 满足要求。
振动方程
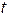(2) 当 = π/4 s时代入速度和加速度表达式，有
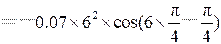
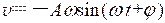
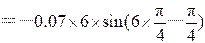
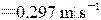
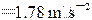
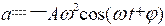
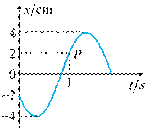
例2已知简谐振动曲线如图所示，试写出其振动方程。
解：解法一：定义法
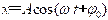设简谐振动方程为
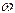
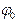
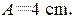只需求出 和 。
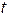
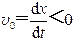
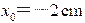=0时，
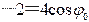且 （由曲线的斜率决定），代入振动方程，有 ，故
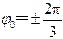
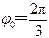
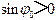
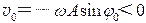又由于 得 故
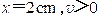
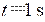
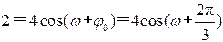再从图中分析可得 时， ，代入振动方程有
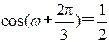即
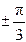
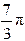
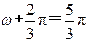
所以 或 （注意这里不能取 ）
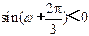
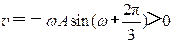
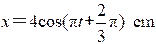
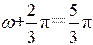因为 ，即
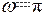所以 ，即 ，所求振动方程为
解法二：旋转矢量法
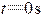
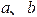
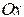
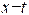如图所示，在 曲线的左侧作 轴与位移坐标轴平行，由振动曲线可知， 两点对应于 、1s时刻的振动状态，可确定这两个时刻旋转矢量的位置分别为Oa和Ob。
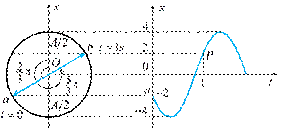
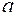
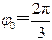
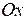
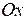
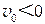
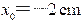
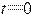
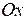向 轴作垂线，其交点就是 时刻旋转矢量端点的投影点。已知该处 ，且此时刻 ，故旋转矢量应在 轴左侧，它与 轴正向的夹角 ，即初相位；
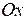
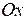
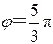
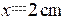
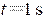
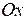
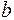
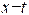又由 曲线中 点向 轴作垂线，其交点就是 时刻旋转矢量端点的投影点，该处 且
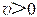，故此时刻旋转矢量应在 轴的右侧，它与 轴的夹角
就是该时刻的振动相位，即
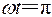
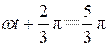
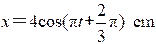最后由于圆半径是4 cm（简谐振动的振幅），所求振动方程是
【教学策略】讲练结合，深化学生对物理知识的理解和巩固，充分调动学生学习的积极性和主动性，提升学生思考、分析问题的能力。
四、内容小结、拓展提升
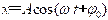内容小结（1）简谐振动的运动学方程：
（2）描述简谐振动的三个重要参量：
振幅
周期、频率、角频率
相位和初相位
（3）旋转矢量表示法
思考提升（学习通发布任务）：结合自身专业，收集简谐振动在生产生活中的应用事例。
拓展阅读（相位命名来历和类比法）：在一个月内月亮由新月（朔）经上月到满月（望），再由满月经下弦月到新月。朔望和上下弦等称为“月相”，月相这种周而复始的变化与简谐振动的相位很相似，中译名“相位”的“相”字来自于“月相”表示状态。让学生体会中华文化的博大精深，建立学生对我国的文化自信。利用旋转矢量法求出简谐振动方程的简便方法类比在遇到问题时，要学会通过“已知”探索“未知”。感知解决问题多途径，处理问题要敢于另辟蹊径，培养学生的创新性思维。
【教学策略】①“内容小结”巩固所学知识，激发学生乐学、善学、会学、爱学的热情与自信；②“拓展阅读”引导学生查阅资料，了解相位命名的来历和体会寻求简单解决问题的方法和途径，培养学生具有创新性思维。
五、教学总结
本节的教学内容简谐振动的运动学，其教学重点是简谐振动中的三个重要参量(振幅、周期、位相和初位相)、简谐振动的旋转矢量表示法，会由已知条件利用解析法或旋转矢量法求出简谐振动方程。
在教学中，将物理知识与现代科技前沿以及日常生活相联系，激发学生学习的积极性，通过由浅入深的讨论，引导学生思考和探究，提高学生发现问题、分析问题、解决问题的能力。教学过程中引入相位命名的来历和利用旋转矢量法求解谐振动微分方程通解的简便方法，建立学生的文化自信和培养创新性思维。
